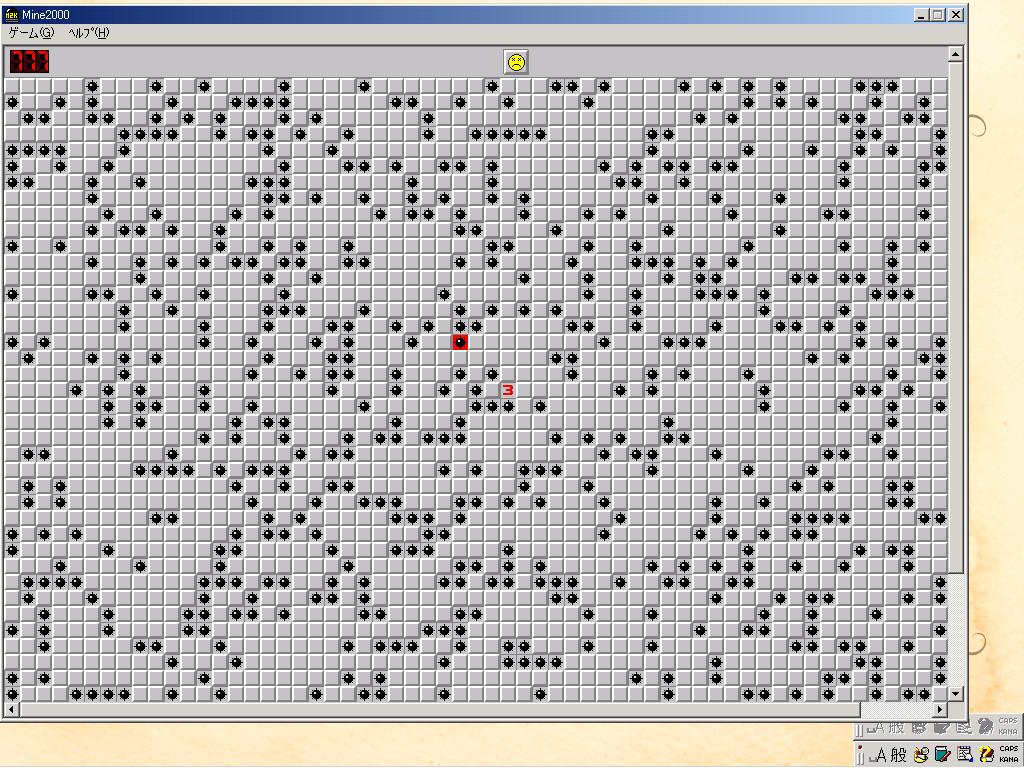
ゲームの分析

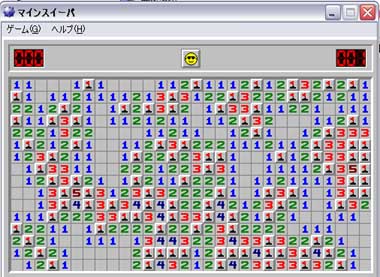
パターン
ゲーム中には、あるマスに地雷があるかどうか断定できる数多くのパターンが存在する。
すでに地雷の位置が定まったところを処理し、その後でまだ定まらないところを処理するのが大抵は最も簡単である。
不確定なマスが存在する場合、特にこれは重要である。
なぜなら、断定できるマスから推理を進めていくことで、いずれ不確定なマスが不確定でなくなる可能性があるためである。
例えば、直角の角に相当する部分のマスに対して、その斜めに隣接するマスが1となっていれば、その角は地雷である。
これはパターンの中でも一番簡単な例であるが、他にも数多くのパターンがある。
より地雷の多い盤面では、マスを開いた時、たまに数字の8を見つけることがある。
その場合、そのマスはすべて地雷に囲まれている。
また、フィールドの辺に隣接する5や角にある3も、周りが爆弾で囲まれていることを意味する。
平らな壁の中ほどに接した3のマスがあれば、その場所を中心に一列に3つの地雷が並ぶ。
1の隣に2があるような壁では、その2の斜め向かいで1から離れた側に地雷がある。
数字の2が両側を1に挟まれて現れるような壁では、真ん中に接するマスには地雷はない。
なぜなら、もしそのマスに地雷があるとすれば、下段中央の2に隣接している地雷の数が2であるためには、上段両端のマスのうち、どちらか片方のみに地雷があるということになる。
そうなれば、下段両端の1のうち、地雷があった方のマスには2つの地雷が隣接することになり、矛盾するからである。
壁に2がずらっと並んでいる場合、まず4つの2が両端を1で挟まれていると、真ん中の2つの2に接するマスと両端の2つの1に接するマスに地雷がある。
また、5つの2が同じように両端を1で挟まれていると、中央以外の2に接するマスに地雷がある。
これらのパターンは、1つか2つの2が1に挟まれているパターンを拡張したものであり、それら短いパターンと同じ原則によって地雷が配置されている。
フィールドの境界から垂直に伸びる壁の根元の2つが2であれば、それらに接するマスは地雷である。
これは境界に接した2に2つの隣接した地雷を配置できる唯一の可能性だからである。
フィールドの境界から垂直に伸びる壁の根元の2つが1であれば、根元から3つ目のマスに接するマスは地雷ではない。
これは境界に接した1のために根元から2つ目までのマスに接したマスのどちらかに必ず地雷が1つあり、2番目の1が表す地雷の位置もそのどちらかのマスに定まってしまうからである。

盤面の難易度の測定

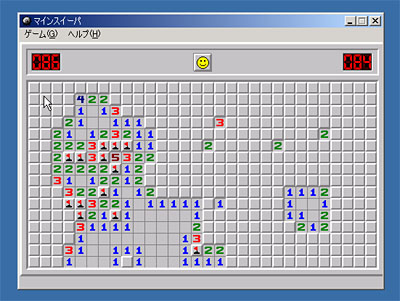
マインスイーパの盤面の難易度は、しばしば3BVの値によって判定される。

3BV

Stephan Bechtelはマインスイーパの盤面をクリアするために必要な最少左クリック数を数えた最初の人物だと考えられている。
2002年6月、彼はこの方法をマインスイーパのゲストブックに書き込んだ。
すぐに、Benny Benjaminはこの方法の名前として3BVという用語を作った。
そしてその後の2ヶ月間で、Yoni RollとBenny Benjaminはマインスイーパの盤面の画像を分析し、その盤面の3BVを示す「Minesweeper Board Reader」という名前のプログラムを作成した。
2003年、Sorin Maneaはマインスイーパのプレイを記録するプログラムを改良し、クリック回数だけでなくその盤面の3BVを表示するようにした。
これはプレイした盤面の3BV/s（1秒間あたりの3BV）を計算した最初のプログラムでもあった。
2004年、Rodrigo Silveiraは盤面に3BVを表示する能力、生成する盤面の3BVの範囲を選択する能力、クリアした盤面の3BVの統計をすべてひとつのファイルに保存する能力のような、3BVに関連したたくさんの特徴を持つ「Minesweeper Clone」を発表した。
プレイの履歴を表現するより簡単な方法のおかげで、ある3BVでの盤面（クリアした盤面限定）の分布を分析することができる。
また、生成した盤面の3BVの分布の表を表示することのできるプログラムもあった。

3BV

▲Page Top